Scroll to:
A MODIFIED MCDM ALGORITHM WITH CUMULATIVE ENTROPY WEIGHTS FOR SELECTING THE WINNER OF THE TENDER
https://doi.org/10.17747/2618-947X-2019-1-46-51
Abstract
The aim of this research is to evaluate the proposed bids using impartial and entropy weights in a multi-criteria decision-making model. We use matrix data for hypothetical bidding involving nine criteria, with the presence of four domestic and two foreign contractors. Then, using cumulative entropy function, we estimate the entropy weights and use it in a multi-criteria decision-making model. The criteria of experience and knowledge in the field, good history and satisfaction in previous projects, financial and support capabilities, localization of the contractor, having the experience at the site of the project, availability and readiness of equipment and machines, the adequacy of technical staff, the work quality system, the efficient management and appropriate management system, creativity and innovation in similar tasks are the input variables of the decision model. After analyzing them, the proposals are prioritized through a multi-criteria decision-making model. The research findings include Shannon entropy and cumulative entropy-based weights for evaluation criteria and after applying the specific weight for the proposed quotation, the utility rate of each contractor is calculated. The results showed that the use of modified multi-dimensional decision-making method is more advantageous than traditional methods of evaluating bidding proposals in selecting the winner of a tender, and also using cumulative entropy weights in comparison with Shannon's leads to a more realistic choice of contractors.
For citations:
Matin A.O., Misagh F. A MODIFIED MCDM ALGORITHM WITH CUMULATIVE ENTROPY WEIGHTS FOR SELECTING THE WINNER OF THE TENDER. Strategic decisions and risk management. 2019;10(1):46-51. https://doi.org/10.17747/2618-947X-2019-1-46-51
INTRODUCTION
The evaluation of a bid is considered by the bidder, contractors and the evaluation committee of the proposal. Traditionally, the quote value is used as the indicator of the bidding process, which is not difficult to understand its simplicity. Experience has shown that the winners of the bidding may not have the ability to complete the assigned duties and Leave the job halfway. In order to overcome this problem, it is essential that the contractors' eligibility criteria be considered in the evaluation of the bidding process. In this paper, we present a modified multi-criteria decision-making model with impartial weights of information measures.
Traditionally, multivariate statistical methods are used to evaluate and rank the performances in the financial analysis (Diak- oulaki, Mavrotas, Papayannakis, 1992). These methods are not suitable, due to unrealistic assumptions and their dependence on a single performance criterion, for today's dynamic business environment.
Data Envelopment Analysis (DEA) (Chames, Cooper, Rhodes, 1978) has attracted much attention for evaluation and ranking. The evaluation of large commercial banks with multiple inputs and outputs is discussed in (Chames, Cooper, Sun, et al., 1990) using DEA. It is also shown in (Shannon, 1948) that it can be used to compare varied products of various sizes.
Some researchers believe that DEA is more efficient and useful in evaluating companies than common approaches (Smith, 1990). Nevertheless, the primary objective of data envelopment analysis is to identify the existence and absence of inactivity and the inefficiency of companies and to rank their sub-aspects (Stewart, 1996). In addition, the selection of inputs and outputs that are included in the evaluation process is often confronted with problems (Boussofiane, Dyson, Thanassoulis, 1991).
Recently, multi-criteria analysis or decision-making has been widely used in choosing, taking into account several criteria of evaluation, the optimal among available options as well as ranking them. With multi-dimensional characteristics of proposers in tenders, this method provides an efficient framework for comparing them with respect to their various abilities and anticipates their overall performance.
The entropy weights with modified TOPSIS are used to compare and rank companies in (Deng, Chung-Hsing, Robert, 2000). By applying entropy in the decision-making model, the effect of inherent auto-correlation of financial incorporate ranking is reduced. A risk measure based on entropy is introduced in (Yang, Qiu, 2005) for generating generalized decision-making models. With that risk measure, they have succeeded in solving some problems that cannot be solved with classical models. A dynamic decision model has been introduced in (Wang, Zhan, 2012) for evaluating proposals at auctions, which used Shannon entropy as weights.
The entropy method for determination of weight considers adequately the information of values all the monitoring sections provided to balance the relationship among numerous evaluating objects. This weakens the bad effect of some abnormal values and makes the result of evaluation more accurate and reasonable.
Entropy method can compute unbiased relative criteria weights and enables measuring the source and determining the relative weights of criteria in a simple and straightforward manner.
Shannon entropy has been used in different branches of science, and statisticians have played a crucial role in the evolution of the information theory framework for solving statistical problems. When entropy was presented by Shannon (Shannon, 1948), it turned out that entropy can be interpreted as the size of the missing information or the increase in uncertainty when the system changes stochastically. A comprehensive list of entropy applications can be found in (Mittelhammer, Judge, Miller, 2000), which also provides basic material for economics and econometrics.
The concept of residual cumulative entropy is introduced in (Wang, Vemuri, Rao et al. (2003). The duality of it has been investigated in (Di Crescenzo, Longobardi, 2009) for measuring the uncertainty in elapsed time and it has also been discussed its relationship with residual cumulative entropy. The weighted cumulative entropy was introduced by (Misagh, Yari, Famoosh, 2011) and its nonparametric estimators with a full review of its features were presented in (Misagh, 2016). In this paper, with the development of these articles, we will use cumulative entropy to construct impartial weights to modify the multi-criteria decision-making model.
Previous studies on entropy and its role in multi-criteria decision-making focus only on the density and probabilities of the criteria.The traditional entropy method focuses on discrimination among data to determine attribute weights. If an attribute can discriminate the data more effectively, it is given a higher weight. In this paper, we will solve a multi-criteria decision problem using the sample mean, variance and ordered statistics in the form of cumulative entropy weights. The proposed quote will also have a specific weight rather than other evaluation criteria.
RESEARCH METHOD
In a problem of reviewing the proposals, the options or participants are already known to decide on them. After determining the criteria, it has to be clear how they will be used to determine the utility of each bidder for winning the tender. In practice, a matrix consists of proposers and criteria with proposals in rows and criteria in its columns. The decision maker enters in each cell of the matrix consistent numerical value for the quantitative criteria and their respective rank for the qualitative ones.
Each criterion has its own measurement scale and, therefore, it is impossible to compare them with each other. They should be measured in a way independent of the unit in order to be compared. To do this, we use the linear standardization method. After standardizing each criterion, their relative importance is determined relative to each other. In fact, we are looking to calculate the amount of information, which is estimated by entropy, in each criterion to solve the decision problem.
In the linear method of standardization, first, we reverse the values of the negative criteria and then divide each value of the column into its maximum. If all of them have a negative aspect, there is no need to calculate the inverse of each of the values, and it is possible (in addition to the previous method) to divide the value of each cell to the maximum value of the column and subtract the yield from one. In the case of reviewing bids, the criteria may be positive (profit) or negative (loss), which x' ij= xij ⁄ max xij and x' ij= (1 ⁄ xij) ⁄ max (1⁄xij) are used to standardize them respectively.
2.1. SHANNON ENTROPY WEIGHTING
The basic idea is based on the fact that the more dispersion in the values of one criterion, the more important it is. To calculate the weights of the criteria, it is considered the probability of i-th
proposal for the j-th criterion as 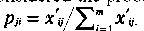 . Shannon entropy of j-th criterion is calculated as
. Shannon entropy of j-th criterion is calculated as 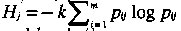 in which the logarithmic basis is optional and k = 1 ⁄ log m.
in which the logarithmic basis is optional and k = 1 ⁄ log m.
The value of dj = 1– Hj is called the uncertainty or the degree of deviation for the j-th criterion, and at last, its entropy weight is obtained from 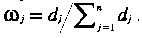 . It should be noted that
. It should be noted that 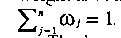 .
.
The largest possible value for Hj equals one and it is obtained when all options in the j-th criterion have equal odds. In this case, it has no useful information about the proposals of the bid. If there is a clear difference between proposals, then the amount of entropy decreases, while the entropy weight should be a large number. Therefore, it is logical to use dj
instead of Hj to calculate the entropy weight.
2.2. CUMULATIVE ENTROPY WEIGHING
In this section, in analogy with Shannon entropy, empirical cumulative entropy is used to weigh the criteria. First, we rewrite the entropy estimators that were presented in (Misagh, 2016; Misagh, Yari, Farnoosh, 2011). Suppose that X(1) ≤ X(2) … ≤ X(m) is a non-descending ordered sample of size m, then the functions
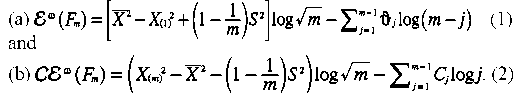
are known as nonparametric estimations of cumulative entropy where
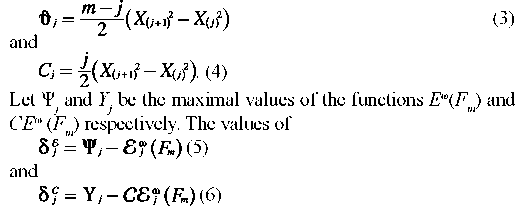
represent the uncertainty or degree of deviation for the j-th criterion.
The weight of the cumulative entropy proportional to the functions εω (Fm) and CEω (Fm), for the j-th criterion, are

respectively. The entropy weight ωj is obtained by the mean of ωj E and ωj C, i.e.

If the decision maker already considers the specific weights λj for the j-th criterion, then the adjusted weight will be as follows

The specific weights λj may be announced by the national and state organs to the bidding process.
2.3. MODIFIED DECISION-MAKING ALGORITHM
In a tender, in addition to the technical and qualification criteria of the contractors, the proposed quotation is considered as an important criterion in the decision-making process. In this section, a step by step algorithm is presented for evaluating the proposers of a tender in four consecutive steps.
Step 1: The set of m proposers is evaluated with respect to a set of n criteria. Consequently, a matrix mxn takes up which is called the performance or decision matrix. Proposers are in its rows and criteria in columns.
Step 2: Standardize the decision matrix to eliminate the effects of different dimensions.
Step 3: Determine the impartial weight of each criterion according to sections (2-1) and (2-2). In each column the greater the difference between the elements, then more information will be transmitted by the criterion and the entropy weight will also increase.
Step 4: Let Ti and T0 be respectively the suggested quote and the tender's base budget, then we define 1 – (Ti⁄ T0) as the quote weights and Ti/ T0 as the weight of the othem criteria. It is assumed that the quotation is less than the tender's base budget, and the larger Ti than T0 will result in the withdrawal of that bid from the evaluation process.
In a bidding process of a tender, the smaller Ti/ T0, then the more chance of winning the bid. Therefore, we use the weight 1 – (Ti⁄ T0) for the standard quote Ti' and Ti/ T0 for other n criteria as a whole while the weight of the information contained in the criteria is determined by entropy. If ωj is the entropy weight of j-th criterion, then the desirability of each proposal will be obtained from the equation
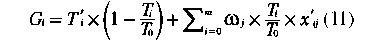
and the proposer with the maximum desirability will be selected as the winner.
If there are already specific weights for the criteria, then in Gi, instead of ωj, ωj* is used.
Specific weights are usually communicated to tenderers by national and state orgaizations.
FINDINGS
In this section, we implement the modified multi-criteria decision-making method for a set of six hypothetical proposers. Necessary criteria of experience and knowledge in the field (executive background), good record and satisfaction in previous work, financial and supportability, availability of ready-made equipment and machinery, efficient and appropriate management system, the adequacy of the technical staff, creativity and innovation in similar work, localization of contractor and experience in the project location are considered for evaluating contractors. Niese criteria are indicated by the symbols C1, C2, C3 C4 C5 C6 C7 C8 and C9 respectively.
The score of each bidder is executed in accordance with the instructions issued by the government authorities and the bidding committee. In order to support the domestic economy against foreign contractors, in many countries competition between participants is made after a percentage deduction from the rates of foreign contractors. In this research, the foreign companies score is reduced by 10% and then the decision is made.
As pointed out at the end of (2-2), the national and state organs may announce some specific weights to the criteria of contractors in the bidding process. These weights are presented in Table 1.
Table 2 presents the raw and standardized values of a hypothetical decision matrix. For each proposer, the raw score is in the first row and the standard values are in the last. The values in the middle row of foreign companies are calculated after deducting ten percent of the main points. The tender's basic budget is considered to be one thousand units.
According to the section (2) and the scores depicted in table 2, impartial weights of Shannon and Cumulative entropies are estimated. They are presented in tables 3 and 4 respectively.
We now calculate the weight of each criterion according to the predetermined specific weights that were depicted in Table I. Final weights are shown in Table 4. Finally, due to the function G_i in Section (2-3), the desirability of each proposer is estimated and presented in Table 5. The desirability of the proposers is shown in the two criteria of Shannon and cumulative entropy in the radar diagram of Figure 1. According to Shannon entropy, the desirability of the third and fourth proposers is more than their desirability based on cumulative entropy. This arrangement is different for others.
Table 1
Criteria and specific weights in a tender
Description | Notation | Speciflc weights |
|---|---|---|
Experience and knowledge in the field (executive background) | V | 20 |
Good record and satisfaction in previous work | V | 15 |
Financial and support ability | V | 15 |
Availability and readiness of equipment and machines | V | 15 |
Efficient management and appropriate management system | V | 10 |
The adequacy of the technical staff and key elements | V | 10 |
The quality system of work | V | 5 |
Creativity and innovation in similar work | V | 5 |
Localization of contractor and experience in the project location | V | 5 |
Quotation or suggested price | T | - |
Table 2
A hypothetical decision matrix
Proposers | Nationality | T | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 |
|---|---|---|---|---|---|---|---|---|---|---|---|
I | Domestic | 900 | 13 | 90 | 9 | 9 | 8 | 8 | 9 | 8 | 70 |
I | 0.84 | I | 0.9 | I | 0.98 | 0.88 | I | 0.88 | 0.7 | ||
II | Domestic | 800 | 10 | 70 | 7 | 7 | 7 | 7 | 7 | 8 | 100 |
0.888 | 0.65 | 0.77 | 0.7 | 0.77 | 0.86 | 0.77 | 0.77 | 0.88 | I | ||
III | Domestic | 850 | 11 | 75 | 8 | 8 | 8 | 9 | 8 | 9 | 100 |
0.944 | 0.71 | 0.83 | 0.8 | 0.88 | 0.98 | I | 0.88 | I | I | ||
IV |
Foreign
| 700 | 15 | 90 | 9 | 8 | 8 | 9 | 10 | 8 | 60 |
700 | 13.5 | 81 | 8.1 | 7.2 | 7.2 | 8.1 | 9 | 7.2 | 54 | ||
0.777 | 0.88 | 0.9 | 0.81 | 0.8 | 0.88 | 0.9 | I | 0.8 | 0.54 | ||
V |
Foreign
| 750 | 17 | 85 | 10 | 9 | 9 | 8 | 9 | 9 | 30 |
750 | 15.3 | 76.5 | 9 | 8.1 | 8.1 | 7.2 | 8.1 | 8 | 27 | ||
0.823 | I | 0.85 | 0.9 | 0.9 | I | 0.8 | 0.9 | 0.88 | 0.27 | ||
VI | Domestic | 900 | 12 | 85 | 10 | 8 | 7 | 8 | 8 | 7 | 70 |
I | 0.78 | 0.94 | I | 0.88 | 0.86 | 0.88 | 0.88 | 0.77 | 0.7 |
CONCLUSION
In the process of evaluating proposals in a tender, instead of the traditional approach, scientific approaches should be used. In this paper, a four-step modified algorithm was introduced with weights of cumulative entropy. Traditional methods of decision making are simple and usually available but also unbiased. Viewing the contractors through a black-and-white lens is deceptive and crafty, especially in a world where conditions change quickly and decision makers have to integrate useful information as much as possible to navigate ambiguous, unreliable and uncertain situations. The new proposed algorithm does not have the shortcomings of traditional ones and it uses, along with the weight of the quotation, impartial weights to extract the information of the decision criteria. Actually, it helps decision makers to avoid subjectivity and arbitrariness which traditional methods suffer from it.
Shannon entropy and most of the uncertainty measure do not take into account the values of criteria. The newly presented criteria weights in (2-2) are functions of the sample mean, sample variance, and order statistics to estimate the uncertainty and reliability so that higher weight is assigned to large values of observations. The latter mentioned property and consistency of estimators (I) and (2) is studied in (Misagh, 2016). Furthermore, the newly introduced algorithm in (2-3) provides the conditions where the main concern of decision-makers in terms of lower budget allocation, along with superior quality criteria, is addressed.
Table 3 Shannon entropy weights
Entropy based index | C1 | C2 | C3 | C1 | C5 | C6 | C7 | C8 | C9 |
|---|---|---|---|---|---|---|---|---|---|
Hj | 0.9947 | 0.9981 | 0.9966 | 0.9981 | 0.9989 | 0.9981 | 0.9980 | 0.9982 | 0.9595 |
dj | 0.0053 | 0.0019 | 0.0034 | 0.0019 | 0.0011 | 0.0019 | 0.00197 | 0.0018 | 0.0405 |
ωj | 0.0885 | 0.031927 | 0.0579 | 0.0318 | 0.0194 | 0.0318 | 0.0327 | 0.0314 | 0.6742 |
Table 4 Cumulative entropy weights
Entropy based index | C1 | C2 | C3 | C1 | C5 | C6 | C7 | C8 | C9 |
|---|---|---|---|---|---|---|---|---|---|
ωEj | 0.118 | 0.089 | 0.127 | 0.080 | 0.059 | 0.080 | 0.128 | 0.078 | 0.241 |
ωCj | 0.156 | 0.097 | 0.121 | 0.112 | 0.048 | 0.112 | 0.060 | 0.115 | 0.180 |
ωj | 0.137 | 0.093 | 0.124 | 0.096 | 0.053 | 0.096 | 0.094 | 0.097 | 0.211 |
Table 5 Final weights for bidding
Weight | Entropy | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 |
|---|---|---|---|---|---|---|---|---|---|---|
ω* | Shannon | 0.2268 | 0.0613 | 0.1114 | 0.0611 | 0.0249 | 0.0408 | 0.0210 | 0.0201 | 0.4321 |
Cumulative | 0.250 | 0.128 | 0.170 | 0.132 | 0.049 | 0.088 | 0.043 | 0.044 | 0.096 |
Table 6 Desirability of proposers
Weight | Entropy | Proposers | |||||
|---|---|---|---|---|---|---|---|
I | II | III | IV | V | VI | ||
Gi | Shamion | 0.663 | 0.732 | 0.763 | 0.6 | 0.522 | 0.657 |
Cumulative | 0.7196 | 0.6581 | 0.7148 | 0.6609 | 0.6607 | 0.7013 | |
Figure 1. Radar diagram for desirability of proposers
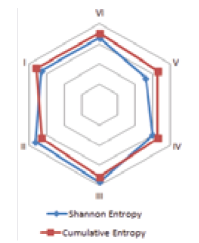
Table 7 shows the status of bidding proposals in two types of Shannon and cumulative entropy weighting. The winning bidder is contractor three by weights of Shannon and is the first one by cumulative entropy weighing.
Although the fourth proposer is considered to be the winner on the basis of the quotation, this position is owned by Contractor Number three using Shannon Entropy.
By comparing their capabilities in Table 2, it can be seen that, although Contractor No. 3 proposed a higher quotation than Contractor No. 4, the latter has a competitive ability as a domestic company. Considering the five criteria of equipment and machinery availability, efficient management and appropriate management system, the adequacy of the technical staff and key elements, creativity and innovation in similar tasks, and the native nature of the contractor, it is superior to Contractor No. 4 or is in an almost identical situation.
Also, the winning place in the weight of cumulative entropy belongs to number one. By comparing the capabilities of the first and third proposers, they are seen to be equal in terms of the appropriate management system, but the first contractor is more powerful than the third one in terms of good record and satisfaction in previous projects, financial and support capabilities, equipment and machine availability, the work quality system. In fact, the contractor chosen by Shannon Entropy deserves only three criteria of nine. It should be noted that the difference in quotation between these two is negligible.
Table 7 Status of bidding proposals
Proposer | I | II | III | IV | V | VI | |
|---|---|---|---|---|---|---|---|
quote | 900 | 800 | 850 | 700 | 750 | 900 | |
Rank of quotation | 5.5 | 3 | 4 | 1 (Winner) | 2 | 5.5 | |
Entropy
| Shamion | 3 | 2 | 1 (Winner) | 5 | 6 | 4 |
Cumulative | 1 (Winner) | 6 | 2 | 4 | 5 | 3 | |
Finally, the comparison of their capabilities shows that the first contractor has a high priority over most criteria than the third one and is more powerful. The multi-criteria modified decision-making method with both entropy-based weightings (Shannon or Cumulative) is successful in choosing the winner of the bid rather than the traditional way (winning choice of the quote), and if two proposers have an equal quotation, There is no choice but to use the impartial weights. It should be noted that the proposed method based on cumulative entropy has not been discussed before in the literature of information theory as well as the literature of multi-criteria decision making.
References
1. Boussofiane, A., Dyson, R. G., Thanassoulis, E. (1991). Applied data envelopment analysis. European Journal of Operational Research. 52 (1):1–15. DOI: 10.1016?/?0377–2217 (91)90331?O.
2. Charnes, A., Cooper, W. W., Rhodes, E. (1978). Measuring the efficiency of decision-making units. European Journal of Operational Research. 2 (6):429–444. DOI: https://doi.org?/?10.1016?/?0377–2217 (78) 90138–8.
3. Charnes, A., Cooper, W. W., Sun, D. B. et al. (1990). Polyhedral cone-ratio DEA models with an illustrative application to large commercial bank. Journal of Econometrics. 46:73–91. DOI: https://doi.org?/?10.1016?/?0304–4076 (90) 90048?X.
4. Deng, H., Chung-Hsing, Y., Robert, J. W. (2000). Inter-company comparison using modified TOPSIS with objective weights. Computers & Operations Research. 27 (10):963–973. DOI: 10.1016?/?S0305–0548 (99) 00069–6.
5. Diakoulaki, D., Mavrotas, G., Papayannakis, L. (1992). A multicriteria approach for evaluating the performance of industrial firms. Omega. 20 (4):467–474. DOI: 10.1016?/?0305–0483(92)90021?X.
6. Di Crescenzo, A., Longobardi, M. (2009). On cumulative entropies. J. of Stat. Plann.& Infer. 139:4072–4087. DOI: 10.1016?/?j.jspi.2009.05.038.
7. Mittelhammer, R. C., Judge, G. G., Miller, D. J. (2000). Econometric foundation. Cambridge, Cambridge University Press.
8. Shannon, C. E. (1948). A mathematical theory of communication. Bell Syst. Tech. J. 27(3):379–423. DOI: https://doi.org?/?10.1002?/?j.1538–7305.1948.tb01338.x.
9. Smith, P. (1990). Data envelopment analysis applied to financial statements. Omega. 18(2):131–138. DOI: https://doi.org?/?10.1016?/?0305–0483(90)90060?M.
10. Stewart, T. J. (1996). Relationships between data envelopment analysis and multi-criteria decision analysis. Journal of Operational Research Society. 47:654–665. DOI: 10.1057?/?jors.1996.77.
11. Wang, W., Zhan, W. (2012). Dynamic Engineering Multi-criteria Decision Making Model Optimized by Entropy Weight for Evaluating Bid. Systems Engineering Procedia. 5:49–54. DOI: 10.1016?/?j.sepro.2012.04.008.
12. Wang, F. E., Vemuri, B.?C., Rao, M. et al. (2003). A new and robust information theoretic measure and its application to image alignment. In: International Conference on Information Processing in Medical Imaging, 3880–4000. Ambleside. Berlin: Springer. DOI: 10.1007?/?978–3–540–45087-0_33.
13. Yang, J. P., Qiu, W. H. (2005). A measure of risk and a decision-making model based on expected utility and entropy. European Journal of Operational Research. 164(3):792–799.
14. Misagh, F. (2016). On Shift Dependent Cumulative Entropy Measures. International Journal of Mathematics and Mathematical Sciences. 1–8. DOI: 10.1155?/?2016?/?7213285.
15. Misagh, F., Yari, G. H., Farnoosh, R. (2011). Weighted Cumulative Entropy and its Estimation. In: Proc. IEEE ICQR. 477–480.
About the Authors
A. O. MatinRussian Federation
Ph.D, Professor, Department of Industrial Engineering, Tabriz Branch, Islamic Azad University, Tabriz, Iran
F. Misagh
Russian Federation
Ph.D, Professor, Department of Statistics, Tabriz Branch, Islamic Azad University, Tabriz, Iran
Competing Interests: Тебризский филиал Исламского университета Азад, Тебриз, Иран
Review
For citations:
Matin A.O., Misagh F. A MODIFIED MCDM ALGORITHM WITH CUMULATIVE ENTROPY WEIGHTS FOR SELECTING THE WINNER OF THE TENDER. Strategic decisions and risk management. 2019;10(1):46-51. https://doi.org/10.17747/2618-947X-2019-1-46-51









































