MATHEMATICAL FORMALIZATION OF INSTITUTIONS

INTRODUCTION

In previous studies we proposed an approach for strategic management based on parametric management where the aspiration to achieve targeted sustainable states and functioning modes is provided by formal institutions [Obydenov A. Yu., 2016b; 2017].

The approach, which considers institutions as a tool of parametric control, sets the task for finding appropriate ways of institutions’ mathematical formalization¹ through their mathematical representation. There appear the problem of formal mapping of a set of institutions onto a set of their representations. Our proposed method of institutions’ mathematical mapping can facilitate the institutions’ mathematical formalization for the purposes of parametric strategic management.

AU ways of describing institutions are divided into explicit and implicit. In the first case, formal components of institutions are described, in the second one, quantitative and qualitative economic consequences of the institutions’ use. The first examples of an explicit description of institutions are contained in the Flerodotus’ treatises (see, example: [Flerodotus, 1972]). One of the modem attempts of explicit algebraic formalization of the institution was undertaken by V. Tambovtsev (2004).

An implicit form of describing an institution is specific for microeconomic analysis. The example of such description is analyzed, for instance, in the study of D. Bromley [Bromley D. W., 1989, p. 111-115]. Weusedtheanalytical microeconomic approach to determine the consequences of institution’s self-regulation [Kryuchkova RV., Obydenov A.Yu., 2003]. The game-theoretic way of describing institutions is also possible: institutions are taken as fixed rules [ Shubik M., 1982], represented by stable strategies in repeating games [Schotter A., 1981]. Flowever, such approaches do not allow to consider institutions as parameters that control the object state (the ratio of gains in the payment matrix). The proposed method of both explicit and implicit algebraic representation of institutions is relevant due to the fact that it meets the requirements of the parametric approach [A. Obydenov, 2016b; 2017].

ALGEBRAIC FORMALIZATION OF INSTITUTIONS. DISCRETE MODEL

We begin with an implicit approach. It proposes the representation of rules through the consequences of their application in matrix games. Consider the case of a symmetric game 2x2:

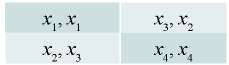
We consider that the applying of the rule leads to changes in the distribution of gains in the payment matrix. You can represent X₁, i = 1,4 as independent coordinates of an algebraic vector in the phase space:

X will define the state of the system, but the action of the rule is the possible transition of the system from one state to another. We represent the rule as an operator R, and thus we proceed to an explicit description of the rules.

Let suppose that in a number of cases within the framework of the dynamic problem, in particular, for analyzing equilibrium points in pure strategies, the ratio of elements X'. is important. That’s why it is enough to represent R as a permutation of the components of an algebraic vector X

For X₁ > X₂ > X₄ > X₃ we obtain a pure coordination game with two Nash equilibriums (coordination problem²) (X₁ = X for X₁ > X₂ > X₄ > X₃).

For X₂ > X₁ > X₄ > X₃ a “prisoner dilemma” is appeared with a single Nash equilibrium that is non-optimal by Pareto (the problem of cooperation) (X₂ =X for X₂ > X₁ > X₄ > X₃).

For X₁ > X₂ > X₃ > X₄ we are dealing with a game where the Nash equilibrium coincides with the Pareto equilibrium (the Nash equilibrium is Pareto optimal) (X₂ =X for X₁ > X₂ > X₃ > X₄).

Formally, the action of the rule can be represented as:

where R- is the permutation operator.

We introduce the designation: R₁₃ = R:X₁ |→X₃, then for the above-mentioned cases we have:

Ihe rule matrix is:

Permutations can be represented as disjoint cycles (in this case, as an elementary transposition), from here: R₁₃ = (3,4).

So, the rule R₁₃ converts a parametrically controlled system from state X₁ to state X' The rule representation is a permutation operator. You can use the known properties of permutations that automatically apply to the rules.

The permutation matrixes are orthogonal. They form a group.

The reverse matrix is equal to the transposed one. Thus, the rules form a group of transformations. In particular the opposite rule implies, which cancels this. The representation matrix of the inverse rule is transposed with respect to the original one. The rule applied the same number of times, which is equal to the group order, returns the system to the initial state.

It should be noted that the chosen form of the algebraic representation of the rule does not allow us to establish a one-to-one correspondence between the rule and its representation. Generally speaking, each representation is degenerate: it corresponds to a set (class) of rules.

Let consider a permutation, which is characterized by a single operator E. This permutation will correspond to a whole class of such rules and under which the action on the payment matrix in the form of permutations of payments will leave unchanged the relations between payments.

We assume that from the point of view of the influence on the equilibrium in the game the action of the institutions leaves the ratio of gains unchanged, thereby do not have the coordination economic consequences of the game situation and therefore are purely distributive. Permutations that are representations of the rules leave the constant amount of each player's gains for all possible strategies. From the economic point of view, the expected payoff (weighted average gain) remains unchanged for each participant. Such weighted average gain is equal to one- fourth of the sum of the gains for any participant. The participants’ possibility for choosing each of the possible strategies in the game is 0.5. In this context, the action of such rule can be called coordination.

Definition. The action of the rule is called coordinating as weighted average gain. As a result of its application, the sum of each participant’s gains for all possible strategies remains unchanged.

The ways of separation the rules effects on coordination and distribution may be different and may be several of them. In this case, the choice of a particular method of division requires an agreement, a convention. The above-mentioned argument suggests one way of this separation.

CONTINUOUS KINETIC MODEL

Let it be some event that can take place with the cooperative behavior of particular group members.

Then for calculation the expected participants’ gains of following cooperative and non-cooperative strategies can be written as respectively following relationships:

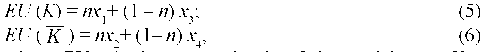
wnere EU - is tne expected gam ot tne participants; A - cooperative strategy; n - is the share of participants of following cooperative strategy; x. - gains in the original payment matrix.

The average (weighted) gain participant is:

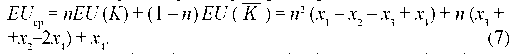
Then, starting trom tne replication equalization m tne framework of evolutionary game theory (in fact this equalization is reflected in the first equality of relation (8)) of the kinetic equalization for n as an independent variable can be written [Hofbauer J., Sigmund Κ., 2003; Smith J. М., 1982; Golman R., Page S. E., 2010; Bierman, El.S.,Fernandez L, 1998, p. 384-397]:

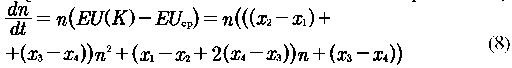
As control parameters we introduce .O = X₁- X₀ and b = x - X₄. Then in the framework of the simultaneous game we have considered above in pure strategies:

• for a > 0, b < 0 there are two Nash equilibriums (pure coordination game, coordination problem);
• for a < 0, b < 0 one Nash equilibrium, different from Pareto equilibrium (prisoner's dilemma, problem of cooperation);
• for a > 0, b > 0 oone Nash equilibrium, coinciding with the Pareto optimal.

As the initial situation before applying the parametric control we consider the case a > 0, b < 0. Then this equalization which is solved relatively has three roots (0, b/(b - a), I).

If now the equalization

And in the framework of the evolutionary game from (8) we get:

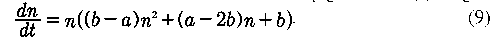
As the initial situation before applying the parametric control we consider the case a > 0, b < 0. Then this equalization which is solved relatively has three roots (0, b/(b - a), 1).

If now the equalization

where Q - is the volume of released production by the economic entity, which describes the management model of the economic entity behavior in the framework of the strong form of the rationality bounded hypothesis (Obydenov A. Yu., 2017) and normalized to the roots Q₂ = 0,5 and Q₃ = I (instead of roots O₂ = 1 and O₃ = 2), Then instead of this equalization (10) we get:

And if in equalization (9) we put a= 0,5; b = -0,5, then we obtain an equalization up to designation that is identical to equalization (11):

In the phase diagram we obtain two stable points: n₁ = 0, n₃ = 1 and one unstable: n₂ = 0,5.

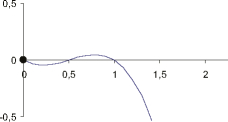
Thus, in different ways we obtained identical equalizations with identical roots. In both cases, there are two stable states that create opportunities for parametric control. We know that this case (a > 0, b < 0) with continuous O and n corresponds to a simultaneous coordination game in pure strategies with two Nash equilibriums. This example illustrates the “popular theorem”: in pure strategies of simultaneous play with strict Nash equilibriums in the evolutionary game within the dynamic’s replication correspond to attractors (asymptotically stable states) [Cressman R., 2003].

We put for implementation parametric control in ratio to (12) in (9) a = I, b = 0 (one Nash equilibrium, Pareto optimal) and we obtain the kinetic equalization:

We have one stable state n = 1:

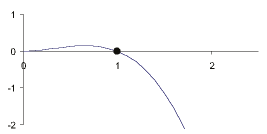
In the framework of the strong form’s model hypothesis about the bounded rationality of such control corresponds to price regulation [Obydenov A.Yu., 2017]. From the point of view of game theory with a = I, b = 0 we have a simultaneous game with one Nash equilibrium in pure strategies that can be Pareto optimal. Such parametric control corresponds to a rule (institution) with a matrix which specified in equalization (4).

Based on the identity of equalizations (11) and (12), the similarity of the equalization after control (13) we conclude that different tasks in formulation terms lead to identical descriptions, similar control methods and their results. Earlier, we have already noted that similarities between the kinetic equalization in the framework of the strong form model of bounded rationality (equalization 11) and the equation obtained on the basis of evolutionary game theory (equalization 12). Similarities are caused by availability of scale advantage and proportionality to the benefits of changing the independent variable in both cases. In the strong form model of bounded rationality the role of the game-theoretic average gain plays a normal profit per unit of production. In both cases, there is a multiplicity of stable states. AU these similarities (see table) allow us to summarize the results of the research.

In general, we can talk about the effect of coordination [Polterovich V.M., 1999, p. 8-9]. For example, if more people follow the mental model, the norm then the less profitable the deviation from the norm becomes and the benefit becomes greater for everyone who adheres to this model of behavior or norm. Some researchers call this effect the “herd effect” [Dixit A. K., Nalebuff B. J., 1991].

Thus, the considered nonlinear dynamics with three stationary states is generally characteristic of the coordination problem and various coordination tasks correspond to such dynamics: for example, the evolution of the traffic direction rule [Kuzminov Ya. I., Bendukidze KA, Yudkevich MM ., 2006], a model of the evolution of the QWERTY rule, the dynamics of the neighborhood of the white and African American population in American cities [Dixit, Nalebuff, 1991]. Such behavior is specified for active (self-organizing) bistable environments [A. Loskutov, A. S. Mikhailov, 2007]. In this case, our approach may be effective for solving problems of coordination in general.

CONCLUSION

Institutions can be represented as permutations of gains of economic entities within the framework of the game-theoretic approach. Such an algebraic formalization of institutions helps to investigate the properties of institutions through their controlling influence on the economic situation. In particular it will be possible to distinguish more strictly between the coordination and distribution aspects of the institutions’ functioning, to identify situations in the practice of managing when a set of established rules leads to an identical transformation and also to combine the rules that produce the same action into classes.

The use of the formalism of the evolutionary theory of games allows us to move from simultaneous discrete games to parametric control in the framework of nonlinear dynamic models. Nonlinear dynamics with three stationary states is found in a wide variety of models. The proposed method of formalizing institutions can be used to solve a sufficiently wide range of tasks, for example, to present institutions as parameters that allow you to manage the self-organization of economic entities strategically in particular by changing the structure of steady states in situations with a problem of coordination.