ЦЕЛЕВОЕ ПЛАНИРОВАНИЕ В КОНТЕКСТЕ УПРАВЛЕНИЯ ФИНАНСОВЫМ РАЗВИТИЕМ БАНКОВ

Введение

За последние годы в период социально-эко­номических перемен задача обеспечения устой­чивого развития банковских систем стран СНГ, в том числе и Украины, в целом и задача управ­ления финансовым развитием отдельного банка в частности актуальны благодаря тому, что функ­ционирование банковских систем сопровождает­ся проявлением разного рода кризисных явлений в финансовой деятельности банков. Анализируя сегодня ситуацию, в которой находятся банки Украины, можно говорить о несовершенстве си­стем управления финансовым развитием банков, оптимального планирования финансового раз­вития банков, прогнозирования и предупрежде­ния кризисных явлений, целевого планирования финансовой деятельности банков. Эти и другие факты стали причинами того, что для некоторых украинских банков появилась перспектива бан­кротства.

В современных условиях большое значение имеет вопрос оптимизации процесса управления финансовыми ресурсами банков и поиска гибких подходов к управлению их финансовым развитием в целях оперативного и адекватного реагирова­ния как на внутренние, так и на внешние факто­ры, которые влияют на финансовую деятельность банка и на его развитие в целом. Актуальными задачами являются предотвращение ухудшения финансового состояния банка, нахождение пу­тей оптимального распределения ресурсов путем оптимизации финансовых показателей банка и в результате обеспечение эффективного процесса управления финансовым развитием банка.

Исходя из вышесказанного важным вопросом является формирование управления, способного обеспечить как эффективное финансовое разви­тие банка, так и адекватное реагирование банка на влияние дестабилизирующих факторов внеш­ней и внутренней среды. При этом остро стоит проблема целевого планирования, то есть опреде­ления ориентиров финансовых показателей дея­тельности банка при управлении его финансовым развитием.

Анализ последних исследовании и публикаций

Существенный вклад в разработку теории и практики управления в банках внесли такие украинские ученые, как В. И. Мищенко, Т. С. Смовженко, А.И. Барановский, А. Н. Тридед, С. Н. Козьменко, Л. А. Примостка, Г. М. Азаренко- ва, А.А. Епифанов, И. В. Волошко, А. С. Любунь, И. В. Сало и др., и российские исследователи О.   И. Лаврушин, В. И. Колесников, В. В. Плато­нов, Η. Н. Куницина, Л. И. Ушвицкий, В. В. Пя- тенко, Ю. С. Масленченков и др.

Основное внимание многие ученые и прак­тики уделяют разработке и внедрению методик и рекомендаций относительно стратегического управления банком в целом. В то же время недо­статочно полно рассмотрены методологические аспекты процесса оптимизации финансовых по­казателей банка в ходе управления его финансо­вым развитием. Требуют доработки вопросы оп­тимального планирования финансового развития банков и формирования адекватных критериев и оптимизации финансовых показателей деятель­ности банков с помощью регулярных методов оптимизации Хука - Дживса, Нелдера - Мида, Розенброка, Пауелла, Коши, Ньютона и др. [I, 6]. Поиск примеров использования классических ме­тодов оптимизации в банковском деле для реше­ния задач управления, в том числе и указанных, в научной литературе, библиотеках и Интернете, не дает позитивных результатов. Это позволяет утверждать, что в современном банковском деле нет работ, в которых рассматривались бы методы оптимизации применительно к задачам банков­ского управления, отсутствует описание их тео­ретического и практического применения, такой результативный и мощный математический ап­парат, как методы оптимизации.

Цель исследования

В рамках данного исследования задача со­стоит в оптимизации финансовых показателей деятельности банка в целях I) повышения их значений до эталонных и 2) повышения позиции конкретного банка в общем рейтинге по сравне­нию с банками-конкурентами.

Постановка задачи оптимизации финансовых показателей банка

Оптимум принимаемых решений и планов, разрабатываемых при подготовке действий, а также эффективное использование ресурсов невозможны без корректного математического моделирования финансового состояния банка и прогнозирования обстановки, без сопоставле­ния и оценки возможных вариантов с помощью математического аппарата и новейших инфор­мационных технологий. В общем виде задача математического программирования или зада­ча оптимизации ставится следующим образом [I, 5, 6]. Нужно найти экстремум функции

где xj,x₂,...,x_N - варьируемые переменные или управляемые параметры; h_k - множество ограничений типа равенств; к - номер ограниче­ния типа равенства; К- количество ограничений в виде равенств; G_r - множество ограничений типа неравенств; г - номер ограничения типа не­равенства; R - количество ограничений в виде неравенств; X_θmin - нижнее предельное значение варьируемой переменной; χ_θ - варьируемая пе­ременная; X_θmax верхнее предельное значение варьируемой переменной.

Следует отметить, что некоторые перемен­ные 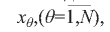 в N-мерном векторном аргу­менте X могут быть равными нулю, то есть не принимать участие в математическом описании ограничений типа равенств (2) и неравенств (3). Кроме того, сами варьируемые переменные в конкретной банковской задаче также изменяются в соответствующих пределах своих возможных минимаксных значений (см. неравенство (4)).

Значения финансовых показателей деятель­ности банков составляют некоторую матрицу P (i-й вектор-столбец элементов матрицы P -список значении однородного г-го показателя для каждого из b банков, а s-й вектор-строка элемен­тов - список разнородных значений показателей для s-го банка (i=1,n);n- количество показателей, которые рассматриваются или участвуют в той или иной методике; s=1,b; b- количество иссле­дуемых банков).

Нормированные значения показателей дея­тельности банка определяются как элементы ма­трицы [3,4]:

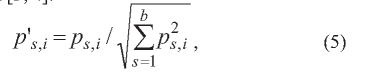
где p_{s i} - численное значение г-го показателя (i=1,n) по s-му банку (s=1,b).

Для формирования эталонного банка [3], к показателям которого в идеальном случае долж­ны приближаться показатели всех других банков, определяются оптимальные значения нормализо­ванных г-х показателей по всем банкам. Под опти­мальными понимаются максимальные или мини­мальные значения соответственно в зависимости от направления влияния на результирующий при­знак. Выбранные нормированные оптимальные значения формируют матрицу-строку [3]:

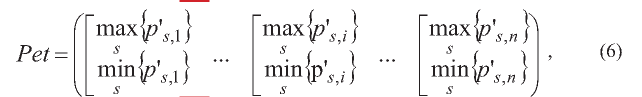
где Pet - матрица-строка значений показате­лей эталонного банка; max{p'_si} -максимальное нормированное значение г-го показателя для всех s банков; min {p's j}- минимальное нормированное значение г-го показателя для всех s банков.

Для сравнения значений г-х показателей всех исследуемых банков с их эталонными значениями используется соотношение между показателями s-го банка и эталонного для определения расстоя­ний D_s согласно с выражением [2, 3]:

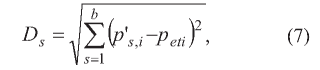
где P_{s i} - нормализованные значения показа­телей деятельности банков; P_eti - значения по­казателей эталонного банка - элементы матрицы- строки (6) {s=1,b; i=1,n).

На базе соотношения (7) построим функцио­нал для оптимизации варьируемых параметров 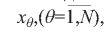, от которых, в свою очередь, зависят финансовые показатели p_{s i} = p_{s i}(x) деятельности конкретного банка и, соответственно, их нормиро­ванные значения P_{s i} = P_{s i} (х) . Здесь еще раз сле­дует акцентировать внимание на том, что в общем случае не все переменные χ_θ,(θ=1,Ν) N-мерного векторного аргумента х могут принимать участие в описании функций p_si = p_si(x) и p'_Sii=p'_Sii (х) и в математическом описании ограничений типа равенств (2) и неравенств (3).

Таким образом, функционал Dj(x), минимум которого необходимо найти с целью максималь­ного приближения конкретного j-ro банка к эта­лонному банку, будет иметь вид:

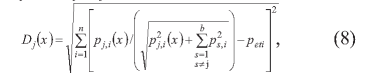
где P_ji - значения i-х показателей для j-ro бан­ка (i =l,n;j=l,b).

У функционала (8) значения финансовых по­казателей p_si деятельности банков не являются функциями варьируемых переменных 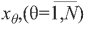, если s≠j. В случае, если s=j, то есть p_si(x)= p_ji(x), для j-ro банка функционал D_j(x) зависит от век­тора варьируемых переменных  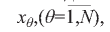и явля­ется аналогом функции-цели (I). Таким образом, поставлена задача оптимизации финансовых по­казателей банковской деятельности в целях повы­шения их значений до эталонных.

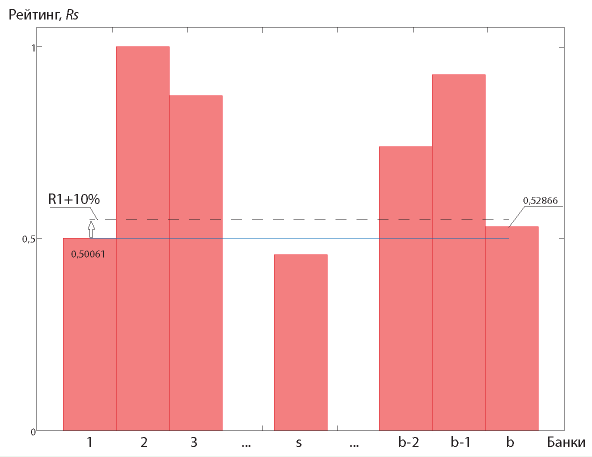
На следующем этапе исследования предлага­ется поставить задачу оптимизации финансовых показателей деятельности банков для решения вопроса о повышении позиции конкретного бан­ка в общем рейтинге, который определен на ос­нове сравнения финансовых показателей группы банков. Допустим, что мы имеем построенный рейтинг Ъ банков. Диаграмма рейтинговых оце­нок в общем случае представлена на рисунке. Необходимо повысить рейтинг конкретного j-ro банка на соответствующий процент, используя оптимизацию финансовых показателей данного банка, на основе которых построен рейтинг, в це­лях улучшения его позиции в общем рейтинге Ь банков. Графически эта задача также изображена на рисунке.

Идея, представленная на рисунке, состоит в том, что перед руководством банка № I, который имеет рейтинговое число R_i = 0.50061, ставится задача повышения своего рейтинга на 10% для опережения банка № b, у которого рейтинговое число R_b = 0,52866. Эту задачу можно решить с использованием мощного аппарата теории опти­мизации.

Рейтинги банков определяются на основе вы­ражения (7): чем меньше значение расстояния D_s, тем выше рейтинг банка. Однако для удобства последующего анализа рейтингов банков и более адекватной детализации полученных данных в графической форме предлагается использовать соотношение, которое характеризует суммарное оейтинговое число R- для каждого из банков:

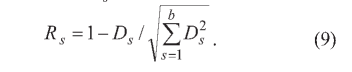
В данном случае чем выше значение суммар­ного рейтингового числа R_s, тем выше рейтинг банка.

Если в нашем случае (см. рисунок) задача ста­вится в повышении рейтинга s-ro банка, напри­мер, на 10%, то соответствующий функционал, который необходимо минимизировать, будет иметь вид:

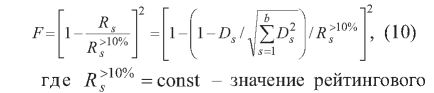
числа для s-го банка, которое увеличено на 10%.

На базе соотношения (10) построим функци­онал для оптимизации варьируемых параметров 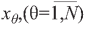 от которых, в свою очередь, зависят финансовые показатели P_si=P_si(x) деятельности конкретного банка и, соответственно, их нор­мированные значения p'_si= p'_si(x). Как и выше, следует отметить, что в общем случае не все переменные  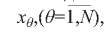N-мерного векторного ар­гумента х могут принимать участие в описании функций P_si=P_si(x) и p'_si= p'_si(x) и в математи­ческом описании ограничений типа равенств (2) и неравенств (3).

Таким образом, функционал, минимум кото­рого необходимо найти для повышения рейтинго­вого числа конкретного j-ro банка на определен­ное количество процентов (в нашем случае 10%, см. рисунок), будет иметь вид:

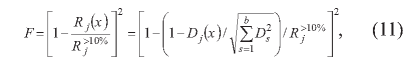
где R_j - значение рейтингового числа для j-ro банка; D_j(x) определяется согласно формуле (8).

В соотношениях (8) и (11) j — индекс, вве­денный для удобства 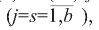 обозначающий номер конкретного банка, рейтинг которого улучшается в процессе оптимизации (в нашем конкретном примере j = I, см. рисунок); D_j(x), R_j(x) определяются по формулам (7) и (9) соот­ветственно. Именно для конкретного j-ro бан­ка осуществляется оптимизация финансовых показателей деятельности, которые зависят от варьируемых параметров 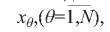. Значения финансовых показателей деятельности всех дру­гих банков группы (s≠j), их рейтинговых чисел R_s(s≠j) и показателей эталонного банка остают­ся неизменными.

В функционалах (8) и (11) значения финан­совых показателей p_si деятельности банков не являются функциями варьируемых переменных 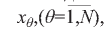 если s≠j, При s=j, то есть p_si(x)= p_ji(x), для j-гo банка функционал F(11) зависит от век­тора варьируемых переменных χ_θ,(θ=1,Ν) и явля­ется аналогом функции-цели (I).

Нулевым приближением [1, 5, 6] для варьи­руемых параметров χ_θ,(θ=1,Ν) является вектор х_θ⁽⁰⁾,(θ = 1;N) > от которого зависят значения фи­нансовых показателей P_ji=P_ji(x⁽⁰⁾) деятельности конкретного банка и, соответственно, их норми­рованные значения P'_ji=P'_ji(x⁽⁰⁾)· При использова­нии регулярных методов оптимизации решением поставленной задачи будет вектор _χθ,(θ= ΪΛ0, ко­торый обеспечивает минимум функционалу (11).

Что касается ограничений задачи оптимиза­ции финансовых показателей деятельности банка вида (2)-(4), то их математическое описание зави­сит от конкретного набора показателей, на основе которого построен текущий рейтинг банков. При этом необходимо отметить, что лицо, принима­ющее решение, может установить ограничения вида (2)-(4) на варьируемые переменные или за­фиксировать некоторые из них в целях постро­ения объективной адекватной математической модели задачи оптимизации финансовых показа­телей деятельности банков. Например условно, если размер капитала банка № I равен 200 млн грн, а для банка № Ъ значение этого показателя равно 4 млрд грн, то очевидно, что варьировать этим показателем или вообще бессмысленно (оп­тимизация будет проводиться по другим показа­телям, варьируя которые можно получить лучший рейтинг банка № I), или необходимо установить адекватные ограничения для этого значения, на­пример в виде ограничений (4). Следует отме­тить, что при фиксировании некоторых перемен­ных Xg_t(O=I_tN) размерность задачи оптимизации уменьшается, то есть снижается количество ва­рьируемых переменных, тогда как с увеличением количества показателей и описывающих их ва­рьируемых переменных размерность задачи опти­мизации возрастает.

Выводы

Поставленные задача оптимизации финан­совых показателей банковской деятельности с целью увеличения их значений до эталонных и задача оптимизации финансовых показателей де­ятельности банков для повышения позиции кон­кретного банка по сравнению с банками-конку- рентами в общем рейтинге представляют собой задачи нелинейного программирования с нели­нейными функционалами и возможными нели­нейными ограничениями. Оптимальные значения переменных, от которых зависят финансовые по­казатели деятельности банков, можно определить с применением классических регулярных методов оптимизации. Эти оптимальные переменные - финансовые показатели деятельности банка - и являются результатом целевого планирования фи­нансовых показателей при управлении финансо­вым развитием банка, на которые должен ориен­тироваться банк в процессе своей деятельности.